Gender pay gap: Is 10% gap large? Not necessarily!

Gender pay gap (GPG) is quite a hot topic (before the era of the coronavirus, of course!) and it is, simply speaking, the difference between the salary of men and women. To make it more precise and to avoid any confusion, one should make a crucial classification of GPG right from the beginning, which is, as often as not, overlooked in the media:

Non-adjusted (uncontrolled) GPG: It compares the mean or median of salaries of men and women (for example in different countries and with different ethnicities), ignoring all or most of their differences (like full/part-time position, years of experience, working hours, different positions in terms of seniority, etc.)

Adjusted (controlled) GPG: This is the difference in the salary for equal work and when the only difference between the groups is gender.

https://www.payscale.com/data/gender-pay-gap

Both of these two types of GPG are worth being studied, however, I should highlight their different applications:

• Adjusted GPG can be used to study gender discrimination in salary because we compare two groups whose main (only) difference is gender.

• Non-adjusted GPG, on the other hand, cannot prove any gender discrimination in salary. There are lots of differences between groups, so, there is no way that it can confirm or reject gender discrimination.

• That being said, the non-adjusted GPG can be used for other purposes, like illustrating that women do not earn as much as men, which can guide us towards understanding the underlying reasons, for example, discrimination against one gender in getting higher positions or in the access to the education (which leads to better-paid jobs). Note that, it does not necessarily do so.

Also, note that the adjusted GPG is far smaller than the non-adjusted one, which could imply that the gender’s direct effect on the earning is smaller than other factors living in the non-adjusted GPG. One may call them indirect effects.

So, hereinafter, whenever I talk about GPG I mean the adjusted gender pay gap when everything is the same between the groups, but the gender! 

How much is too much?

If a reliable source reports GPG for a survey as 1%, do you consider it as “small”? What about 5%? What about 10%?

I would assume that 1% is not really important for most of us. We might think that it is just statistics, no ones expect 0% difference and always there can be a very tiny random detail which changes the numbers. With 5% feminist and women's right activist will be quite upset, and with 10% perhaps most of us!

The simple but surprising truth is that none of these values is meaningful per se! In one survey 1% can show obvious discrimination while, in another survey,  even 10% can be just due to chance, and cannot prove the existence of any gender discrimination!

That was the conclusion I wanted to make out of this post! Now you know the result, let’s explain why it is so! 

Let’s ask help from Mann-Whitney-Wilcoxon Test

Mann-Whitney-Wilcoxon is a statistical test telling us if the difference between the two groups is really significant or it is just due to randomness or chance. So, the survey is likely no to support gender discrimination. Look here for an introduction:

We consider four difference cases: 

• Small GPG which is not significant → not surprising (Example A)
• Small GPG, which is significant  → surprising (Example B)
• Big gap, which is not significant  → surprising (Example C)
• Big gap, which is significant → not surprising (Example D)

Examples B and C are more interesting, as they come with a surprise and contradict our intuition.

Now, we investigate these 4 examples in details. Each example consists of two groups of men and women, each with 25 samples.

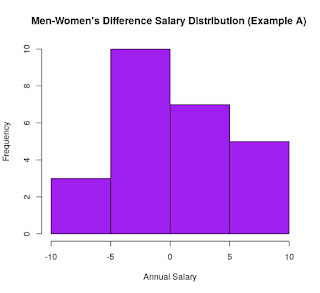
Small GPG which is not significant

The mean difference between groups is 1% in favour of men. Here, you can see the distribution of the salary for each group as well as its difference:

Here is the quantile for each group, which does not show much difference between men and women:

So, quite naturally, one would not expect this small difference to be significant. This guess can be confirmed by the Wilcoxon test:

The main point here is the p-value which shows that if everything was due to the chance, there was a 69% chance that we get a difference as big as this 1% between groups. So, we conclude that this 1% is very likely to due to chance.

Small GPG which is significant

The mean difference between groups is 1% in favour of men. But as you can most men earn quite close to the mean (55 K) and there are few men who earn more:

The quantile also shows a difference between groups, as women's salary is always below men's:

The Wilcoxon test confirms that this small difference is significant, as the p-value is almost zero, which shows that the chance of getting such an extreme and strange case is very small (67 over one trillion!)

Big GPG which is not significant

The mean difference between groups is 12% in favour of men but the variation in men's salary is quite high.

The quantile also confirms that the distribution of men's salaries is quite wide compared to women's:

In fact, this is the reason which makes this big GPG non-significant, as the Wilcoxon test shows:

It says that there is a 20% probability for this to happen simply due to chance, and this is too high to be considered as a real significant difference between the two group! So, even such a high difference may not prove gender discrimination!

Big GPG which is significant

This looks quite expected! The mean difference between groups is 19% in favour of men:

Let's look at the quantile, which shows a quite big difference:

Add caption

Then, the Wilcoxon test confirms that the difference is not likely to happen due to chance as p-value is very small, 0.0002!

What do we get from all these?

We showed that a small difference can be significant while a big difference can be non-significant. So, we should not claim or reject the gender pay gap (or similar difference/discrimination-based statements) only based on the absolute value of a difference! Numbers can be misleading, remember!

How do statistics may lie to us?

Let me start by making my point clear: numbers (so the statistics) do not lie, they simply cannot! Lying is "the act of saying or writing something that is not true, in order to deceive someone, deliberately”. Numbers, do not speak, as far as we are concerned, so they cannot lie!

So, why do I want to talk about how statistics lie while they literally do not? Simply, because I wanted to catch your attention? Partially yes, but also because they still can trick us, to cause us to believe something untrue. This is what we may call an “unintentional lie”, even though for using such a term you could get criticized as it is an oxymoron. 

Let me explain such tricks with a simple example: If you read in a respectable newspaper that

• the average salary in Paris is about 2500 euro per month (net, after taxes and all)

• the average salary in Paris is higher than any other city in France

your brain may, unintentionally, trick you by making you assume that “Woow! One would prefer to live in Paris than province”, knowing that this 2500 euro is far more than the average salary in the rest of France. But is your assumption true? Certainly not. There are lots of rich people working and living in Paris, like well-known doctors, lawyers, and artists who earn your annual salary just in a month, while there are others living with SMIC (minimum wages) and even less!

https://www.courrierinternational.com/sujet/df

In fact, the average salary tricks our brain and gives us the illusion of knowing the income of an average man/woman working in Paris while, somewhere in our brain, we have confused the average salary of the whole of Paris (of rich and poor families) with the average a person can get in Paris! In order to get a more complete overview,  things like the variation between salaries (variance or standard deviation in statistics) and also the living cost of a Parisian should come into play.

So, at the end of the day, it is not the statistics to blame, but us, and our brain. We use statistics to compare and to decide, as the statistics summarize complicated comparison (with lots of factors) into one or two numbers which are easy to understand and to interpret, like the mean (average), and this can mislead us sometimes, as we saw in that example.

This scary “bug” in our understanding of statistics has not been detected only recently; in fact, it has been so infamous that in 1954, Darrell Huff, an American writer, published a best-seller book titled “How to Lie with Statistics” which illustrated simple but important misuses of statistics for the general public. In his book, he explains in a simple language how plots and numbers can do us a bad trick! 

If this problem has been known for since a long time ago, politicians and the people of business were those who benefit it more. They use it almost every day to deceive us into buying our vote, our support or to suck our money!

For example, when Colgate tells you that 

• 80% of dentists recommend Colgate’s toothbrush

they do not lie about the 80% itself, but they do not tell us the setting of the survey: that each dentist could recommend more than one product and Colgate could succeed to get the recommendation from 80% of the surveyed dentists while another brand might have gotten 100% support! And this seemingly unimportant detail will change the whole meaning of the message, doesn’t it?

But things can be more complicated than these quite simple examples: Recently, an article by The Guardian titled “Are female leaders more successful at managing the coronavirus crisis?” got viral in the social network. 

This article describes what women leaders, in Germany, New Zealand, Taiwan and some other countries have done to take the pandemic under the control, and emphasizes on the empathy that they showed towards the society. At one point, the authors claim that

“ … women have managed the coronavirus crisis with aplomb. Plenty of countries with male leaders – Vietnam, the Czech Republic, Greece, Australia – have also done well. But few with female leaders have done badly.”

They do not come into an obvious conclusion; however, the reader may easily assume that the women leader did a better job in handling this crisis. The immediate impression coming out of the article is likely to be a positive answer to the question posed in the title: “Yes! Female leaders are more successful in managing the coronavirus crisis.” This is also compatible with the interpretation of a large part of social media from this article. 

When I read the article, the first thing which came to my mind was the measure by which they decided which country did a good or bad job during this crisis. They did not mention any, even if they really had! My next concern was that the article was flawed in different directions to start with: 

• How can one disregard all the differences between countries, such as the quality and quantity of health care facilities, namely ICU beds per capita, number of tourists visiting the country (in particular from China) and also the role of other parties involved in managing a health crisis, like the Ministry of Health?
• If we assume that country X under the leadership of Mr. Y did a bad job, it seems very unlikely that just by replacing him with Madam W we get a very different outcome, isn’t it? So, probably in the best case, we cannot show anything better than a correlation between having a women leader and well-managing coronavirus. And who does not know that:

Then, I wondered to make such a comparison on my own, just a simplified study to see if what they tried to promote can be roughly justified based on the existing data. Here are some of my assumptions:

• I rely on the data from Our World in Data. Whether or not they are trustable in a country or not is not what I can reject or validate, but to be on the safe side, I prefer not to take the data from China into account.
• I consider the “number of confirmed cases per capita” as the measure to compare the countries: the smaller it is, the better the country could control the spread of the virus. If we do not consider the population of a country, we may reach very counter-intuitive conclusions: A small country whose all inhabitants got contaminated would perform superior to a big country which could limit the cases to 6% of the population! 
• One should be aware that the total number of confirmed cases (per capita or in total) is smaller than the total number of contaminated people, as lots of countries (with men or women leaders) did not do massive testing, unlike South Korea. 
• Some countries, like Sweden, took the herd immunity approach which is, simply speaking, letting virus contaminate the population to create immunity as fast as possible. Whether or not it was a better approach, it is no point in considering these countries into account for this study.

Here is the map for all counties based on the measure I chose:

As one can see in the first glance, the whole western part of Europe is quite dark, while south-east Asia is almost white. And in Oceania, Australia and New Zealand have a similar color To be more precise, we select a couple of countries from North America, Western Europe, Asia and Oceania and try to see if there is any difference between countries  based on the gender of their leader:

Women-led countries

Men-led countries

Excluding Taiwan, it seems that there is no big difference between the countries I have selected. In fact, for women-led countries, we get the average 2496 while for men-led countries this value is smaller 2066! I also compute the quantiles of the data in R and I get:

This confirms my initial guess that for women-led countries Taiwan was quite an exception (we call it an outlier in statistics) and may even get ignored.

So, did men even do better (on average)?

To be honest no! At least, it cannot be justified based on the sample I chose. To confirm it, I do a famous statistical test, the so-called Mann-Whitney-Wilcoxon Test which tells how much the two groups are different and if the difference we observe is significant or it is simply due to chance. In my case, it is the latter which holds:

Why is it so? Because the p-value is large! If p-value was small enough (usually less than 0.01) I could say that the difference between these two groups is significant, but now it tells me that there is 70.21% chance that I could observe the same difference between groups even if everything was based on the chance! 

What can we conclude from all these? 

You may get disappointed, but I would say NOTHING! Some women-led countries (like Taiwan) did a great job, while some others like Iceland did a terrible job! And, based on the measure I chose, men-led countries did a similar job as women-led ones. The statistical test does not confirm any significant difference between these two groups. So, a statistician may not agree with the authors in saying that female leaders had a better performance during this crisis.

For me, it is sad and surprising that after this article being published, instead of getting criticized, it was promoted mostly with positive feedbacks such that others tried similar misleading arguments, like Christiane Amanpour, a CNN's journalist as well as a very recent article in New York Times:

Whatever is their intention of promoting all these deceptive contents, the simple truth is that they are far from being true. It will not help to defend women’s right, achieving gender equality or anything like that. On the one hand, it may damage all genuine attempts of people who work hard towards these holy objectives. On the other hand, it is morally wrong to feed the public with wrong information and “analyses”. Such a wrongful practice will result after a sufficient amount of time, in them to accept these invalid claims as non-refutable facts! In the next article, I will touch, quite carefully and from the statistical point of view, one of these topics: the gender pay gap!